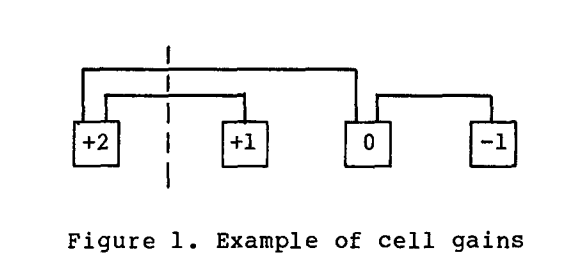
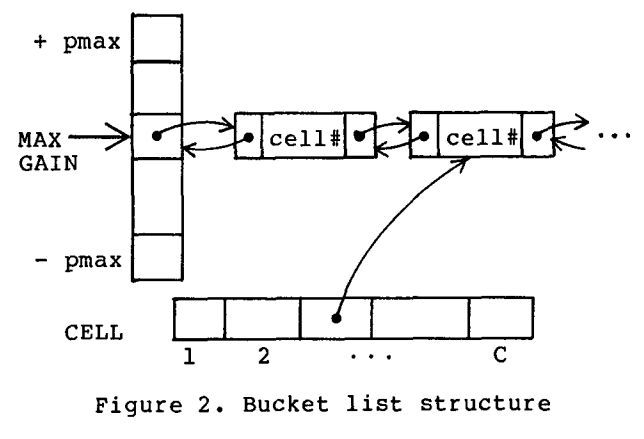
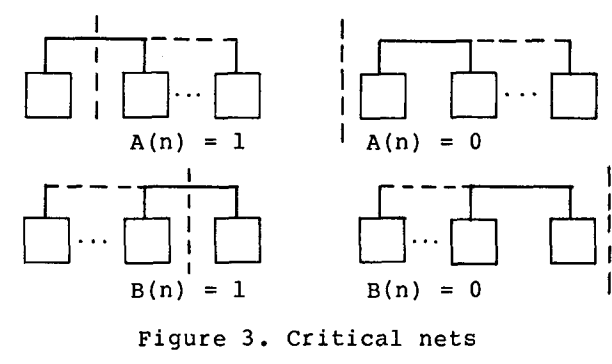
什么是Ioc
Ioc(Inversion of Control)是一种设计模式.它指的是使用某对象/资源的代码,不负责该对象的依赖对象的创建和维护,而交给一个专门的容器来负责.这样,怎么创建对象的控制权就转移到了这个专门的容器,即实现了所谓的控制反转.Ioc用来降低对象之间由依赖关系产生的耦合.(按照软件工程理论,依赖算是最弱的一种耦合了.依赖 < 关联 < 聚合 < 组合< 继承)我感觉,Ioc算是一个升级版的工厂模式,它管理了大量的工厂函数和对应的资源名称.可以把创建资源/对象的依赖写在Ioc里面.
adonisjs5中的Ioc
我感觉有点奇怪,adonisjs5的官方文档中没有专门提及Ioc. https://docs.adonisjs.com/guides/introduction 但在adonisjs4.x https://legacy.adonisjs.com/docs/4.1/ioc-container 的官方文档中却有单独的一节来讲Ioc.以至于,我第一次读完adonis5的文档后,对Ioc竟然没什么印象.而Ioc却是adonis最为重要的概念.anyway~,看看adonis的源代码怎么处理Ioc吧.
注册Ioc
在adonisjs的代码中搜索一下,
find node_modules/@adonisjs -iname "*ioc*"
很容易发现adonisjs实现Ioc的代码在node_modules/@adonisjs/fold/build/src/Ioc/这个目录中.目录名就是Ioc,毫不掩饰自己的目的.
逛一逛Ioc这个目录下的js文件,发现最重要的是index.js 和 binBindings.js这两个文件.其中index.js中有一个类就叫Ioc, 而注册到Ioc中的资源被放在Bindings.js文件中Bindings类中.
/**
* Define a binding
*/
register(binding, callback, singleton) {
this.list.set(binding, { callback, singleton });
return this;
}
Binding类中的register函数非常显眼.显然注册一个资源到Ioc的代码会走到这里.在这里下断点,调起调试器.发现register函数的三个参数的含义是: binding即资源的的namespace,通过调试器发现注册的第一个资源的namespace是“Adonis/Core/Application”;callback相当于创建这种资源的工厂函数,调用它即生产出一个对应的对象;而singleton则是一个boolean值,指示该种资源是不是一个单件.看看栈的上一个frame,是Ioc类的singleton()函数.看来,“Adonis/Core/Application”这个资源是通过Ioc.singleton()创建的.
/**
* Same as the [[bind]] method, but registers a singleton only. Singleton's callback
* is invoked only for the first time and then the cached value is used
*/
singleton(binding, callback) {
helpers_2.ensureIsFunction(callback, '"ioc.singleton" expect 2nd argument to be a function');
this.bindings.register(binding, callback, true);
return this;
}
Ioc.singleton()函数注释告诉我们.single()函数跟bind()函数一样,只不过是注册一个单件,单件的callback工厂函数仅调用一次.第一次创建会把资源cache起来,而后直接返回cache.这个cache即Bindings类中的list成员.虽然名字是list,但却是一个Map.映射namespace到对象/资源.
constructor(container) {
this.container = container;
/**
* Registered bindings
*/
this.list = new Map(); // 明明是个Map,为何叫list?misnomer~~
}
在看Ioc.singleton()函数的注释时提到了它的friend, Ioc.bind()函数.于是,在Ioc.bind()中下断点看看.发现了’Adonis/Core/Helpers’的,会调到这里.Helpers竟然不是singleton,有点意外.Ioc.bind()同样会调用Bindings.register()把工厂函数存起来.
/**
* Register a binding with a callback. The callback return value will be
* used when binding is resolved
*/
bind(binding, callback) {
helpers_2.ensureIsFunction(callback, '"ioc.bind" expect 2nd argument to be a function');
this.bindings.register(binding, callback, false);
return this;
}
从Ioc创建对象/资源
最开始看adonisjs4的官方文档 ,提到从Ioc创建对象直接调用Ioc.use(‘namespace’).后来看到adnoisjs的作者(大佬HARMINDER VIRK)写的一篇博客 https://blog.adonisjs.com/introducing-adonisjs-v5/ 中讲他特希望把Ioc的use()干掉,改成用EM的import.但Virk大佬没说use()换成import有什么好处.其实在adonisjs5中,使用use()仍然是可以的。
If I ever wanted to improve something to AdonisJS, that was getting rid of the use method to import dependencies,
…
Finally, we have been able make ESM imports work with the AdonisJS IoC container. It means, you can import bindings from the container as follows:
import Route from '@ioc:Adonis/Core/Route'
大佬Virk还提到,用这种方式不能用alias,理由是IDE会帮你补全名称,所以使用长名字不是一个问题.
那么我们看看import是怎么让Ioc创建对象/资源的.在Bindings类的resolve()函数中下断点:
/**
* Resolve a binding. An exception is raised, if the binding is missing
*/
resolve(binding) {
const bindingNode = this.list.get(binding);
if (!bindingNode) {
throw IocLookupException_1.IocLookupException.lookupFailed(binding);
}
let resolvedValue;
if (bindingNode.singleton) {
bindingNode.cachedValue = bindingNode.cachedValue ?? bindingNode.callback(this.container);
resolvedValue = bindingNode.cachedValue;
}
else {
resolvedValue = bindingNode.callback(this.container);
}
return resolvedValue;
}
这个函数根据namespace的名字创建对象.如果是单件,就返回cache中的原有对象;如果不是就创建一个返回.断点第一次命中是,resolve函数的binding参数是”adonis/Core/Env”.看来拦到了创建“donis/Core/Env”对象的代码.看栈的上一帧是Ioc.resolveBinding(),上上帧则是Ioc.use(),再往上就是import语句
import Env from '@ioc:Adonis/Core/Env'
这~~~import之后就直接到了Ioc.use()!!!魔法呀~~从栈的显示来看import语句被显示成<anonymous>.我猜import应该是被解析成一个特殊的无名函数,而有某种方法可以Hook这个无名函数,让import的时候,模块名前面五个字符是”@ioc:”时,就跳去Ioc.use().
不过,后来我搞懂了这个机制。adonisjs5自己整了一个Typescript的编译器。它提供了一个visitor模式可以访问typescript被编译成javascript的代码结构,并可以做修改。于是,用这个visitor模式可以把import Env from ‘@ioc:Adonis/Core/Env’ 替换成一个Ioc.use()调用,载入对象。这个Typescript编译器在这个工程中:https://github.com/adonisjs/require-ts
只写这么多吧.其实里面的内容还有很多~~